CRPA of SrVO3: Difference between revisions
| (40 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Template: | {{Template:GW - Tutorial}} | ||
The following tutorial describes how to perform [[Constrained–random-phase–approximation_formalism|cRPA calculations]], which is available as of VASP 6. | |||
== Task == | == Task == | ||
Calculation of the Coulomb matrix elements <math>U_{ijkl}(\omega=0)</math> in the constrained Random Phase Approximation ([[Constrained-random-phase approximation|cRPA]]) of SrVO<sub>3</sub> between the Vanadium t<sub>2g</sub> states. | |||
Calculation of the Coulomb matrix elements <math>U_{ijkl}(\omega=0)</math> in the constrained Random Phase Approximation ([[Constrained | |||
---- | ---- | ||
Performing a | Performing a cRPA calculation with VASP is a 3-step procedure: a DFT groundstate calculation, a calculation to obtain a number of virtual orbitals, and the actual cRPA calculation itself. | ||
'''N.B.:''' This example involves quite a number of individual calculations. | '''N.B.:''' This example involves quite a number of individual calculations. | ||
| Line 19: | Line 19: | ||
{{TAGBL|SYSTEM}} = SrVO3 # system name | {{TAGBL|SYSTEM}} = SrVO3 # system name | ||
{{TAGBL|NBANDS}} = 36 # small number | {{TAGBL|NBANDS}} = 36 # small number of bands | ||
{{TAGBL|ISMEAR}} = 0 | {{TAGBL|ISMEAR}} = -1 # Fermi smearing | ||
{{TAGBL|SIGMA}} = 0.1 # electronic temperature in eV (1eV ~ 11604K) | |||
{{TAGBL|EDIFF}} = 1E-8 # high precision for groundstate calculation | {{TAGBL|EDIFF}} = 1E-8 # high precision for groundstate calculation | ||
{{TAGBL|KPAR}} = 2 # parallelization of k-points in two groups | {{TAGBL|KPAR}} = 2 # parallelization of k-points in two groups | ||
| Line 65: | Line 66: | ||
Use following {{TAG|INCAR}} file to increase the number of virtual states and to determine the long-wave limit of the polarizability (stored in {{TAG|WAVEDER}}): | Use following {{TAG|INCAR}} file to increase the number of virtual states and to determine the long-wave limit of the polarizability (stored in {{TAG|WAVEDER}}): | ||
*{{TAG|INCAR}} (see INCAR. | *{{TAG|INCAR}} (see INCAR.PBE) | ||
{{TAGBL|SYSTEM}} = SrVO3 | {{TAGBL|SYSTEM}} = SrVO3 # system name | ||
{{TAGBL|ISMEAR}} = 0 | {{TAGBL|ISMEAR}} = -1 # Fermi smearing | ||
{{TAGBL|KPAR}} = 2 | {{TAGBL|SIGMA}} = 0.1 # electronic temperature in eV (1eV ~ 11604K) | ||
{{TAGBL|ALGO}} = Exact | {{TAGBL|KPAR}} = 2 # parallelization of k-points in two groups | ||
{{TAGBL|NELM}} = 1 | {{TAGBL|ALGO}} = Exact # exact diagonalization | ||
{{TAGBL|NBANDS}} = 96 | {{TAGBL|NELM}} = 1 # one electronic step suffices, since WAVECAR from previous step is present | ||
{{TAGBL|LOPTICS}} = .TRUE. | {{TAGBL|NBANDS}} = 96 # need for a lot of bands in GW | ||
{{TAGBL|LOPTICS}} = .TRUE. # we need d phi/ d k for GW calculations for long-wave limit | |||
{{TAGBL|LFINITE_TEMPERATURE}} = T # compute all optical matrix elements (only required for CRPAR) | |||
Restart VASP. | Restart VASP. | ||
At this stage it is a good idea to make a safety copy of the {{TAG|WAVECAR}} and {{TAG|WAVEDER}} files since we will repeatedly need them in the calculations that follow: | At this stage it is a good idea to make a safety copy of the {{TAG|WAVECAR}} and {{TAG|WAVEDER}} files since we will repeatedly need them in the calculations that follow: | ||
cp {{TAGBL|WAVECAR}} WAVECAR. | cp {{TAGBL|WAVECAR}} WAVECAR.PBE | ||
cp {{TAGBL|WAVEDER}} WAVEDER. | cp {{TAGBL|WAVEDER}} WAVEDER.PBE | ||
== | == cRPA Calculation == | ||
Calculate the | Calculate the cRPA interaction parameters for the t2g states by using the PBE wavefunction as input | ||
cp WAVECAR. | cp WAVECAR.PBE {{TAGBL|WAVECAR}} | ||
cp WAVEDER. | cp WAVEDER.PBE {{TAGBL|WAVEDER}} | ||
*{{TAG| | And use following input file as | ||
*{{TAG|INCAR}} (see INCAR.CRPA) and run vasp | |||
{{TAGBL|SYSTEM}} = SrVO3 # system name | |||
{{TAGBL|ISMEAR}} = -1 # Fermi smearing | |||
{{TAGBL|SIGMA}} = 0.1 # electronic temperature in eV (1eV ~ 11604K) | |||
{{TAGBL|NCSHMEM}} = 1 # switch off shared memory for chi | |||
{{TAGBL|ALGO}} = CRPA # Switch on CRPA | |||
{{TAGBL|NBANDS}} = 96 # CRPA needs many empty states | |||
{{TAGBL|PRECFOCK}} = Fast # fast mode for FFTs | |||
{{TAGBL|NTARGET_STATES}} = 1 2 3 # exclude wannier states 1 - 3 in screening | |||
{{TAGBL|LWRITE_WANPROJ}} = .TRUE. # write wannier projection file | |||
#{{TAGBL|LFINITE_TEMPERATURE}} = T # T>0 formalism can be avoided here, because U computed only at omega=0 | |||
{{NB|warning|As of version 6.2.0 run this tutorial successfully by adding following lines to INCAR. For older version copy wannier90.win.CRPA to wannier90.win and omit following lines in INCAR.}} | |||
{{TAGBL|NUM_WANN}} = 3 | |||
{{TAGBL|WANNIER90_WIN}} = " | |||
num_bands= 96 | num_bands= 96 | ||
# | # because bands 21, 22, 23 do not cross with other bands | ||
# one can exclude all other bands in wannierization | |||
# and omit the definition of an energy window like so | |||
exclude_bands = 1-20, 24-96 | |||
begin projections | begin projections | ||
V:dxy;dxz;dyz | V:dxy;dxz;dyz | ||
end projections | end projections | ||
" | |||
The cRPA interaction values for <math>\omega=0</math> can be found in the {{TAG|OUTCAR}}: | |||
spin components: 1 1, frequency: 0.0000 0.0000 | spin components: 1 1, frequency: 0.0000 0.0000 | ||
screened Coulomb repulsion U_iijj between MLWFs: | screened Coulomb repulsion U_iijj between MLWFs: | ||
1 2 3 | 1 2 3 | ||
1 3. | 1 3.3459 2.3455 2.3455 | ||
2 2. | 2 2.3455 3.3459 2.3455 | ||
3 2. | 3 2.3455 2.3455 3.3459 | ||
screened Coulomb repulsion U_ijji between MLWFs: | screened Coulomb repulsion U_ijji between MLWFs: | ||
1 2 3 | 1 2 3 | ||
1 3. | 1 3.3459 0.4281 0.4281 | ||
2 0. | 2 0.4281 3.3459 0.4281 | ||
3 0. | 3 0.4281 0.4281 3.3459 | ||
screened Coulomb repulsion U_ijij between MLWFs: | screened Coulomb repulsion U_ijij between MLWFs: | ||
1 2 3 | 1 2 3 | ||
1 3. | 1 3.3459 0.4281 0.4281 | ||
2 0. | 2 0.4281 3.3459 0.4281 | ||
3 0. | 3 0.4281 0.4281 3.3459 | ||
averaged interaction parameter | averaged interaction parameter | ||
screened Hubbard U = 3. | screened Hubbard U = 3.3459 0.0000 | ||
screened Hubbard u = 2. | screened Hubbard u = 2.3455 0.0000 | ||
screened Hubbard J = 0. | screened Hubbard J = 0.4281 -0.0000 | ||
The full interaction matrix is written to {{FILE|UIJKL}}. | |||
{{NB|mind|The frequency point <math>\omega</math> can be set by {{TAG|OMEGAMAX}} in the INCAR.}} | |||
For instance to evaluate the cRPA interaction matrix at <math>\omega=10</math> eV, add | |||
{{TAGBL|OMEGAMAX}} = 10 | {{TAGBL|OMEGAMAX}} = 10 | ||
to the INCAR and restart VASP. In contrast, adding following two lines to the {{TAG|INCAR}} | to the INCAR and restart VASP. In contrast, adding following two lines to the {{TAG|INCAR}} | ||
| Line 147: | Line 150: | ||
In addition, the bare Coulomb interaction matrix is calculated for a high {{TAG|VCUTOFF}} and low energy cutoff {{TAG|ENCUTGW}} and written in that order to the {{TAG|OUTCAR}} file. Look for the lines similar to: | In addition, the bare Coulomb interaction matrix is calculated for a high {{TAG|VCUTOFF}} and low energy cutoff {{TAG|ENCUTGW}} and written in that order to the {{TAG|OUTCAR}} file. Look for the lines similar to: | ||
spin components: 1 1 | spin components: 1 1 | ||
bare Coulomb repulsion V_iijj between MLWFs: | bare Coulomb repulsion V_iijj between MLWFs: | ||
1 2 3 | 1 2 3 | ||
| Line 155: | Line 157: | ||
2 15.0984 16.3485 15.0984 | 2 15.0984 16.3485 15.0984 | ||
3 15.0984 15.0984 16.3485 | 3 15.0984 15.0984 16.3485 | ||
bare Coulomb repulsion V_ijji between MLWFs: | bare Coulomb repulsion V_ijji between MLWFs: | ||
1 2 3 | 1 2 3 | ||
| Line 161: | Line 163: | ||
2 0.5351 16.3485 0.5351 | 2 0.5351 16.3485 0.5351 | ||
3 0.5351 0.5351 16.3485 | 3 0.5351 0.5351 16.3485 | ||
bare Coulomb repulsion V_ijij between MLWFs: | bare Coulomb repulsion V_ijij between MLWFs: | ||
1 2 3 | 1 2 3 | ||
| Line 172: | Line 174: | ||
bare Hubbard u = 15.0984 -0.0000 | bare Hubbard u = 15.0984 -0.0000 | ||
bare Hubbard J = 0.5351 0.0000 | bare Hubbard J = 0.5351 0.0000 | ||
Similar to the effectively screened interaction the full output is written to {{FILE|VIJKL}}. | |||
=== | === cRPA calculation on Matsubara axis === | ||
{{NB|mind|Available as of VASP.6.5.2.}} | |||
Note that the same frequency grid is used as for {{TAG|ALGO}}=RPA (RPA correlation energy calculation) and can not be changed directly. | Note that the same frequency grid is used as for {{TAG|ALGO}}=RPA (RPA correlation energy calculation) and can not be changed directly. | ||
To calculate the | To calculate the cRPA interaction for a set of automatically chosen imaginary frequency points use once again the PBE wavefunction as input | ||
cp WAVECAR. | cp WAVECAR.PBE {{TAGBL|WAVECAR}} | ||
cp WAVEDER. | cp WAVEDER.PBE {{TAGBL|WAVEDER}} | ||
Currently, this step requires | Currently, this step requires the {{TAG|WANPROJ}} file from previous step, no wannier90.win file is necessary. | ||
You can also, delete {{TAG|WANPROJ}} and define a wannier projection as in the previous step in the {{FILE|INCAR}}. | |||
Select the space-time | Select the space-time cRPA algorithm with following file: | ||
*{{TAG|INCAR}} (see INCAR.CRPAR) | *{{TAG|INCAR}} (see INCAR.CRPAR) | ||
{{TAGBL|SYSTEM}} = SrVO3 | {{TAGBL|SYSTEM}} = SrVO3 # system name | ||
{{TAGBL|ISMEAR}} = | {{TAGBL|LFINITE_TEMPERATURE}} = T # use finite temperature formalism | ||
{{TAGBL| | {{TAGBL|ISMEAR}} = -1 # required for finite temperature algorithm | ||
{{TAGBL|ALGO}} = CRPAR | {{TAGBL|SIGMA}} = 0.1 # electron temperature in eV (1 eV ~ 11000 K) | ||
{{TAGBL|NBANDS}} = 96 | {{TAGBL|ALGO}} = CRPAR # Switch on CRPA on imaginary axis | ||
{{TAGBL|PRECFOCK}} = Fast | {{TAGBL|NBANDS}} = 96 # CRPA needs many empty states | ||
{{TAGBL|NTARGET_STATES}} = 1 2 3 | {{TAGBL|PRECFOCK}} = Fast # fast mode for FFTs | ||
{{TAGBL|NCRPA_BANDS}} = 21 22 23 | {{TAGBL|NTARGET_STATES}} = 1 2 3 # exclude wannier states 1 - 3 in screening | ||
{{TAGBL|NOMEGA}} = | {{TAGBL|NCRPA_BANDS}} = 21 22 23 # remove bands 21-23 in screening, currently required for space-time algo | ||
{{TAGBL| | {{TAGBL|NOMEGA}} = 8 # use 8 imaginary frequency points | ||
{{TAGBL|NOMEGA_DUMP}} = 0 # write WFULLxxxx.tmp files at omega=0, used for off-centre Coulomb integrals in next step | |||
Run VASP and make a copy of the output file | Run VASP and make a copy of the output file | ||
cp {{TAGBL|OUTCAR}} OUTCAR.CRPAR | cp {{TAGBL|OUTCAR}} OUTCAR.CRPAR | ||
After a successful run, the interaction values are written to the {{TAG|OUTCAR}} file | After a successful run, the interaction values at {{TAGBL|NOMEGA}}+1 frequencies are written to the {{TAG|OUTCAR}} file, where the first point | ||
is always <math>\omega=0</math>: | |||
spin components: 1 1, frequency: 0.0000 0.0000 | |||
screened Coulomb repulsion U_iijj between MLWFs: | screened Coulomb repulsion U_iijj between MLWFs: | ||
1 2 3 | 1 2 3 | ||
1 3. | 1 3.3450 2.3447 2.3447 | ||
2 2. | 2 2.3447 3.3450 2.3447 | ||
3 2. | 3 2.3447 2.3447 3.3450 | ||
... | |||
spin components: 1 1, frequency: 0.0000 109.6955 | |||
screened Coulomb repulsion | screened Coulomb repulsion U_iijj between MLWFs: | ||
1 2 3 | 1 2 3 | ||
1 | 1 15.2510 14.0759 14.0759 | ||
2 | 2 14.0759 15.2510 14.0759 | ||
3 | 3 14.0759 14.0759 15.2510 | ||
The complete matrix at zero frequency is also written to {{FILE|UIJKL}}, while the result at the first frequency point of the minimax grid{{cite|Kaltak:PRB:2020}} is found in {{FILE|UIJKL}}.1 and so on. | |||
==== Optional: Analytic continuation ==== | |||
screened | To obtain the effective interaction on the real frequency axis from the imaginary axis (stored in {{FILE|UIJKL}}.*) following python code can be used in a [https://jupyter.org/ jupyter notebook]: | ||
<syntaxhighlight lang="python" line> | |||
import numpy as np | |||
from scipy.interpolate import AAA | |||
import matplotlib.pyplot as plt | |||
# results stored in NOMEGA dimensional array | |||
nomega=24 | |||
u = np.zeros( nomega, dtype='complex' ) | |||
# one-site indices | |||
idx=[0,40,80 ] | |||
# store one-site bare interaction | |||
v = np.sum( np.loadtxt('VIJKL').T[4][idx] )/len(idx) | |||
for i in range(nomega): | |||
raw = np.loadtxt( 'UIJKL.{omega:d}'.format(omega=i+1) ) | |||
u[i] = np.sum( raw.T[4][idx] + 1j * raw.T[5][idx] ) / len(idx) | |||
# extract omega points | |||
!grep "omega =" UIJKL.{?,??} | awk '{print $5}' > omegas.dat | |||
omegas=np.loadtxt( 'omegas.dat' )*1j | |||
# use AAA algorithm for analytic continuation | |||
u_cont = AAA(omegas,u ) | |||
# plot real part of U and bare interaction V | |||
z = np.linspace( 0, 200, num=1000) | |||
fig, ax = plt.subplots() | |||
ax.plot( z, u_cont(z).real, '-', color='r', label='U') | |||
ax.axhline(y=v, color='b', linestyle='-', label='V') | |||
ax.legend() | |||
# add low-frequency regime as an inset | |||
zlow=np.linspace( 0, 20, num=1000) | |||
inset_ax = ax.inset_axes([0.35, 0.1, 0.6, 0.6]) # [left, bottom, width, height] | |||
inset_ax.plot(zlow, u_cont(zlow), color='red') | |||
plt.xlabel('$\omega$ [eV]') | |||
plt.show() | |||
</syntaxhighlight> | |||
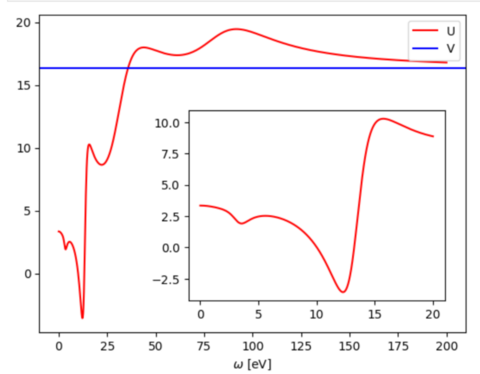
[[File:SrVO3 U omega acont.png|480px]] | |||
{{NB|tip|Increase {{TAG|NOMEGA}} points to resolve more details on the real frequency axis.}} | |||
== Off-centre Coulomb integrals == | |||
Every cRPA job writes the effectively screened Coulomb kernel (in reciprocal space) at zero frequency to {{FILE|WFULLxxxx.tmp}} files. | |||
These files can be read in and off-centre Coulomb integrals can be evaluated using following input: | |||
{{TAGBL|ALGO}} = 2E4WA # Compute off-centre Coulomb integrals | |||
{{TAGBL|ISMEAR}} = -1 # Fermi smearing | |||
{{TAGBL|SIGMA}} = 0.1 # electronic temperature | |||
{{TAGBL|NBANDS}} = 96 # use same number of bands as stored in WAVECAR | |||
{{TAGBL|ALGO}} = 2E4WA # Compute off-centre Coulomb integrals | |||
{{TAGBL|PRECFOCK}} = Fast # fast mode for FFTs | |||
{{TAGBL|NTARGET_STATES}} = 1 2 3 # Wannier states for which Coulomb integrals are evaluated | |||
The bare off-centre Coulomb integrals are written to {{FILE|VRijkl}}, while the effectively screened ones are found in {{FILE|URijkl}}: | |||
# File generated by VASP contains Coulomb matrix elements | |||
# U_ijkl = [ij|kl] | |||
# I J K L RE(U_IJKL) IM(U_IJKL) | |||
# R: 1 0.000000 0.000000 0.000000 | |||
1 1 1 1 3.3450226866 0.0000000000 | |||
2 1 1 1 0.0000058776 0.0000006717 | |||
3 1 1 1 0.0000026927 -0.0000003292 | |||
... | |||
3 3 3 3 3.3450230976 0.0000000000 | |||
# R: 2 0.000000 0.000000 1.000000 | |||
1 1 1 1 0.7321605022 -0.0001554484 | |||
2 1 1 1 0.0000021144 0.0000002295 | |||
... | |||
{{NB|mind|Available as of VASP.6.5.2.}} | |||
== Downloads == | == Downloads == | ||
[ | [[Media:CRPA of SrVO3.zip| CRPA_of_SrVO3.zip]] | ||
{{Template: | {{Template:GW - Tutorial}} | ||
Back to the [[The_VASP_Manual|main page]]. | Back to the [[The_VASP_Manual|main page]]. | ||
[[Category:Examples]] | [[Category:Examples]][[Category:Constrained-random-phase approximation]] | ||
Latest revision as of 09:10, 28 March 2025
The following tutorial describes how to perform cRPA calculations, which is available as of VASP 6.
Task
Calculation of the Coulomb matrix elements in the constrained Random Phase Approximation (cRPA) of SrVO3 between the Vanadium t2g states.
Performing a cRPA calculation with VASP is a 3-step procedure: a DFT groundstate calculation, a calculation to obtain a number of virtual orbitals, and the actual cRPA calculation itself.
N.B.: This example involves quite a number of individual calculations. The easiest way to run this example is to execute:
./doall.sh
In any case, one can consider the doall.sh script to be an overview of the steps described below.
DFT groundstate calculation
The first step is a conventional DFT (in this case PBE) groundstate calculation.
- INCAR (see INCAR.DFT)
SYSTEM = SrVO3 # system name NBANDS = 36 # small number of bands ISMEAR = -1 # Fermi smearing SIGMA = 0.1 # electronic temperature in eV (1eV ~ 11604K) EDIFF = 1E-8 # high precision for groundstate calculation KPAR = 2 # parallelization of k-points in two groups
Copy the aforementioned file to INCAR:
cp INCAR.DFT INCAR
The POSCAR file describes the structure of the system:
SrVO3 3.84652 #cubic fit for 6x6x6 k-points +1.0000000000 +0.0000000000 +0.0000000000 +0.0000000000 +1.0000000000 +0.0000000000 +0.0000000000 +0.0000000000 +1.0000000000 Sr V O 1 1 3 Direct +0.0000000000 +0.0000000000 +0.0000000000 +0.5000000000 +0.5000000000 +0.5000000000 +0.5000000000 +0.5000000000 +0.0000000000 +0.5000000000 +0.0000000000 +0.5000000000 +0.0000000000 +0.5000000000 +0.5000000000
This file remains unchanged in the following.
The KPOINTS file describes how the first Brillouin zone is sampled. In the first step we use a uniform k-point sampling:
Automatically generated mesh 0 Gamma 4 4 4 0 0 0
Mind: this is definitely not dense enough for a high-quality description of SrVO3, but in the interest of speed we will live with it.
Run VASP. If all went well, one should obtain a WAVECAR file containing the PBE wavefunction.
Obtain DFT virtual orbitals and long-wave limit
Use following INCAR file to increase the number of virtual states and to determine the long-wave limit of the polarizability (stored in WAVEDER):
- INCAR (see INCAR.PBE)
SYSTEM = SrVO3 # system name ISMEAR = -1 # Fermi smearing SIGMA = 0.1 # electronic temperature in eV (1eV ~ 11604K) KPAR = 2 # parallelization of k-points in two groups ALGO = Exact # exact diagonalization NELM = 1 # one electronic step suffices, since WAVECAR from previous step is present NBANDS = 96 # need for a lot of bands in GW LOPTICS = .TRUE. # we need d phi/ d k for GW calculations for long-wave limit LFINITE_TEMPERATURE = T # compute all optical matrix elements (only required for CRPAR)
Restart VASP. At this stage it is a good idea to make a safety copy of the WAVECAR and WAVEDER files since we will repeatedly need them in the calculations that follow:
cp WAVECAR WAVECAR.PBE cp WAVEDER WAVEDER.PBE
cRPA Calculation
Calculate the cRPA interaction parameters for the t2g states by using the PBE wavefunction as input
cp WAVECAR.PBE WAVECAR cp WAVEDER.PBE WAVEDER
And use following input file as
- INCAR (see INCAR.CRPA) and run vasp
SYSTEM = SrVO3 # system name ISMEAR = -1 # Fermi smearing SIGMA = 0.1 # electronic temperature in eV (1eV ~ 11604K) NCSHMEM = 1 # switch off shared memory for chi ALGO = CRPA # Switch on CRPA NBANDS = 96 # CRPA needs many empty states PRECFOCK = Fast # fast mode for FFTs NTARGET_STATES = 1 2 3 # exclude wannier states 1 - 3 in screening LWRITE_WANPROJ = .TRUE. # write wannier projection file #LFINITE_TEMPERATURE = T # T>0 formalism can be avoided here, because U computed only at omega=0
| Warning: As of version 6.2.0 run this tutorial successfully by adding following lines to INCAR. For older version copy wannier90.win.CRPA to wannier90.win and omit following lines in INCAR. |
NUM_WANN = 3 WANNIER90_WIN = " num_bands= 96 # because bands 21, 22, 23 do not cross with other bands # one can exclude all other bands in wannierization # and omit the definition of an energy window like so exclude_bands = 1-20, 24-96
begin projections V:dxy;dxz;dyz end projections "
The cRPA interaction values for can be found in the OUTCAR:
spin components: 1 1, frequency: 0.0000 0.0000
screened Coulomb repulsion U_iijj between MLWFs:
1 2 3
1 3.3459 2.3455 2.3455
2 2.3455 3.3459 2.3455
3 2.3455 2.3455 3.3459
screened Coulomb repulsion U_ijji between MLWFs:
1 2 3
1 3.3459 0.4281 0.4281
2 0.4281 3.3459 0.4281
3 0.4281 0.4281 3.3459
screened Coulomb repulsion U_ijij between MLWFs:
1 2 3
1 3.3459 0.4281 0.4281
2 0.4281 3.3459 0.4281
3 0.4281 0.4281 3.3459
averaged interaction parameter
screened Hubbard U = 3.3459 0.0000
screened Hubbard u = 2.3455 0.0000
screened Hubbard J = 0.4281 -0.0000
The full interaction matrix is written to UIJKL.
| Mind: The frequency point can be set by OMEGAMAX in the INCAR. |
For instance to evaluate the cRPA interaction matrix at eV, add
OMEGAMAX = 10
to the INCAR and restart VASP. In contrast, adding following two lines to the INCAR
OMEGAMAX = 10 NOMEGAR = 0
tells VASP to calculate the interaction on the imaginary frequency axis at . This can be used to evaluate at a specific Matsubara frequency point.
In addition, the bare Coulomb interaction matrix is calculated for a high VCUTOFF and low energy cutoff ENCUTGW and written in that order to the OUTCAR file. Look for the lines similar to:
spin components: 1 1
bare Coulomb repulsion V_iijj between MLWFs:
1 2 3
1 16.3485 15.0984 15.0984
2 15.0984 16.3485 15.0984
3 15.0984 15.0984 16.3485
bare Coulomb repulsion V_ijji between MLWFs:
1 2 3
1 16.3485 0.5351 0.5351
2 0.5351 16.3485 0.5351
3 0.5351 0.5351 16.3485
bare Coulomb repulsion V_ijij between MLWFs:
1 2 3
1 16.3485 0.5351 0.5351
2 0.5351 16.3485 0.5351
3 0.5351 0.5351 16.3485
averaged bare interaction
bare Hubbard U = 16.3485 -0.0000
bare Hubbard u = 15.0984 -0.0000
bare Hubbard J = 0.5351 0.0000
Similar to the effectively screened interaction the full output is written to VIJKL.
cRPA calculation on Matsubara axis
| Mind: Available as of VASP.6.5.2. |
Note that the same frequency grid is used as for ALGO=RPA (RPA correlation energy calculation) and can not be changed directly. To calculate the cRPA interaction for a set of automatically chosen imaginary frequency points use once again the PBE wavefunction as input
cp WAVECAR.PBE WAVECAR cp WAVEDER.PBE WAVEDER
Currently, this step requires the WANPROJ file from previous step, no wannier90.win file is necessary. You can also, delete WANPROJ and define a wannier projection as in the previous step in the INCAR.
Select the space-time cRPA algorithm with following file:
- INCAR (see INCAR.CRPAR)
SYSTEM = SrVO3 # system name LFINITE_TEMPERATURE = T # use finite temperature formalism ISMEAR = -1 # required for finite temperature algorithm SIGMA = 0.1 # electron temperature in eV (1 eV ~ 11000 K) ALGO = CRPAR # Switch on CRPA on imaginary axis NBANDS = 96 # CRPA needs many empty states PRECFOCK = Fast # fast mode for FFTs NTARGET_STATES = 1 2 3 # exclude wannier states 1 - 3 in screening NCRPA_BANDS = 21 22 23 # remove bands 21-23 in screening, currently required for space-time algo NOMEGA = 8 # use 8 imaginary frequency points NOMEGA_DUMP = 0 # write WFULLxxxx.tmp files at omega=0, used for off-centre Coulomb integrals in next step
Run VASP and make a copy of the output file
cp OUTCAR OUTCAR.CRPAR
After a successful run, the interaction values at NOMEGA+1 frequencies are written to the OUTCAR file, where the first point is always :
spin components: 1 1, frequency: 0.0000 0.0000
screened Coulomb repulsion U_iijj between MLWFs:
1 2 3
1 3.3450 2.3447 2.3447
2 2.3447 3.3450 2.3447
3 2.3447 2.3447 3.3450
...
spin components: 1 1, frequency: 0.0000 109.6955
screened Coulomb repulsion U_iijj between MLWFs:
1 2 3
1 15.2510 14.0759 14.0759
2 14.0759 15.2510 14.0759
3 14.0759 14.0759 15.2510
The complete matrix at zero frequency is also written to UIJKL, while the result at the first frequency point of the minimax grid[1] is found in UIJKL.1 and so on.
Optional: Analytic continuation
To obtain the effective interaction on the real frequency axis from the imaginary axis (stored in UIJKL.*) following python code can be used in a jupyter notebook:
import numpy as np
from scipy.interpolate import AAA
import matplotlib.pyplot as plt
# results stored in NOMEGA dimensional array
nomega=24
u = np.zeros( nomega, dtype='complex' )
# one-site indices
idx=[0,40,80 ]
# store one-site bare interaction
v = np.sum( np.loadtxt('VIJKL').T[4][idx] )/len(idx)
for i in range(nomega):
raw = np.loadtxt( 'UIJKL.{omega:d}'.format(omega=i+1) )
u[i] = np.sum( raw.T[4][idx] + 1j * raw.T[5][idx] ) / len(idx)
# extract omega points
!grep "omega =" UIJKL.{?,??} | awk '{print $5}' > omegas.dat
omegas=np.loadtxt( 'omegas.dat' )*1j
# use AAA algorithm for analytic continuation
u_cont = AAA(omegas,u )
# plot real part of U and bare interaction V
z = np.linspace( 0, 200, num=1000)
fig, ax = plt.subplots()
ax.plot( z, u_cont(z).real, '-', color='r', label='U')
ax.axhline(y=v, color='b', linestyle='-', label='V')
ax.legend()
# add low-frequency regime as an inset
zlow=np.linspace( 0, 20, num=1000)
inset_ax = ax.inset_axes([0.35, 0.1, 0.6, 0.6]) # [left, bottom, width, height]
inset_ax.plot(zlow, u_cont(zlow), color='red')
plt.xlabel('$\omega$ [eV]')
plt.show()
| Tip: Increase NOMEGA points to resolve more details on the real frequency axis. |
Off-centre Coulomb integrals
Every cRPA job writes the effectively screened Coulomb kernel (in reciprocal space) at zero frequency to WFULLxxxx.tmp files. These files can be read in and off-centre Coulomb integrals can be evaluated using following input:
ALGO = 2E4WA # Compute off-centre Coulomb integrals ISMEAR = -1 # Fermi smearing SIGMA = 0.1 # electronic temperature NBANDS = 96 # use same number of bands as stored in WAVECAR ALGO = 2E4WA # Compute off-centre Coulomb integrals PRECFOCK = Fast # fast mode for FFTs NTARGET_STATES = 1 2 3 # Wannier states for which Coulomb integrals are evaluated
The bare off-centre Coulomb integrals are written to VRijkl, while the effectively screened ones are found in URijkl:
# File generated by VASP contains Coulomb matrix elements # U_ijkl = [ij|kl] # I J K L RE(U_IJKL) IM(U_IJKL) # R: 1 0.000000 0.000000 0.000000 1 1 1 1 3.3450226866 0.0000000000 2 1 1 1 0.0000058776 0.0000006717 3 1 1 1 0.0000026927 -0.0000003292 ... 3 3 3 3 3.3450230976 0.0000000000 # R: 2 0.000000 0.000000 1.000000 1 1 1 1 0.7321605022 -0.0001554484 2 1 1 1 0.0000021144 0.0000002295 ...
| Mind: Available as of VASP.6.5.2. |
Downloads
Back to the main page.